CS224N Lecture 1 Introduction and Word Vectors
Word meaning
Representing words as discrete symbols
在传统NLP中, 我们将word视为离散的符号。特别是one-hot encoding, 如:
其中, 向量维度= 词汇表单词数量(e.g, 500,000)
Problem with words as discrete symbols
- 式2两个向量正交
- 对于one-hot 向量没有相似性的自然理解。
Solution:
替代:学习把相似性编码到向量里。
Representing words by their context
- 语义分布:单词的意思有其频繁出现的近邻词来给定
- 当一个单词w出现在文本中,其上下文是出现在附近的一系列单词( 在一个固定的窗口内)
- 用许多w的文本向量来构建一个w的表示矩阵

Word2vec: Overview
Word2vec (Mikolov et al. 2013 ) 是为了学习词向量的框架。
思路:
- 我们有一个庞大的文本语料库
- 在一个固定词汇表的每个词用一个向量表示
- 在文本中检查每个位置
t,其中有一个中心词c和 上下文词o - 用对于
c和o的词向量的相似度来计算给定中心词c的上下文的概率(或相反) - 调整词向量来最大化这个概率
示例:窗口和处理计算
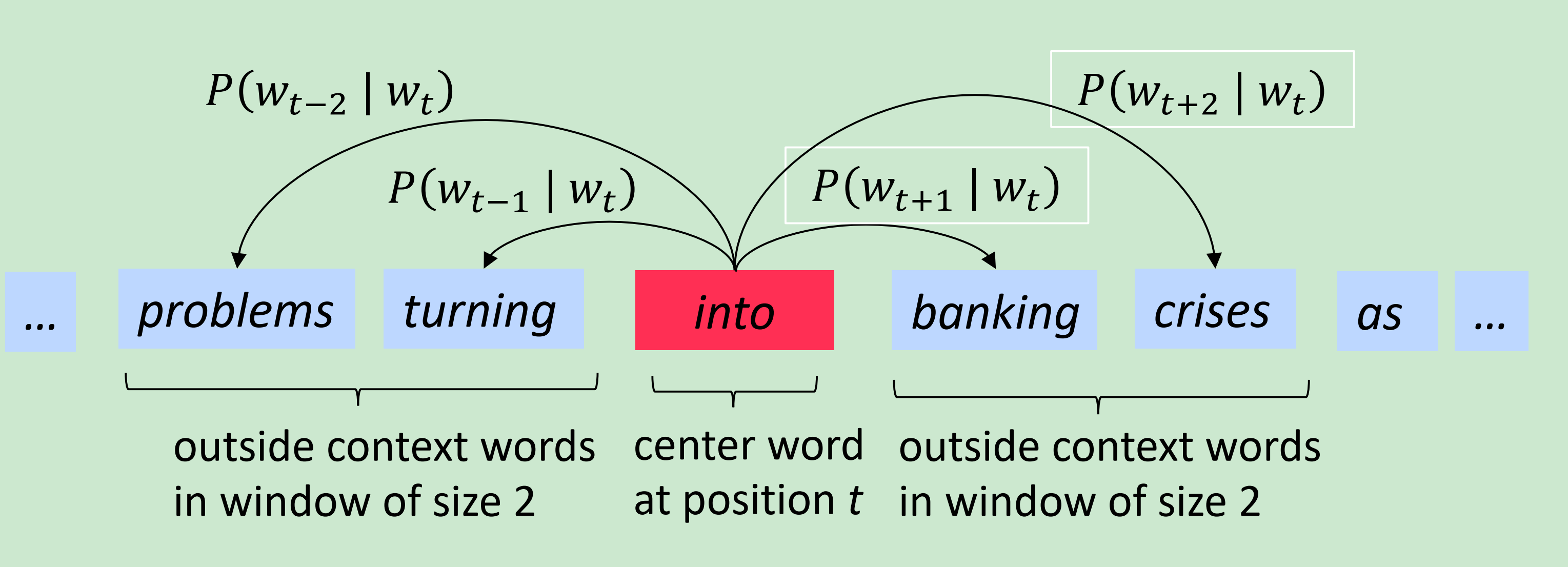
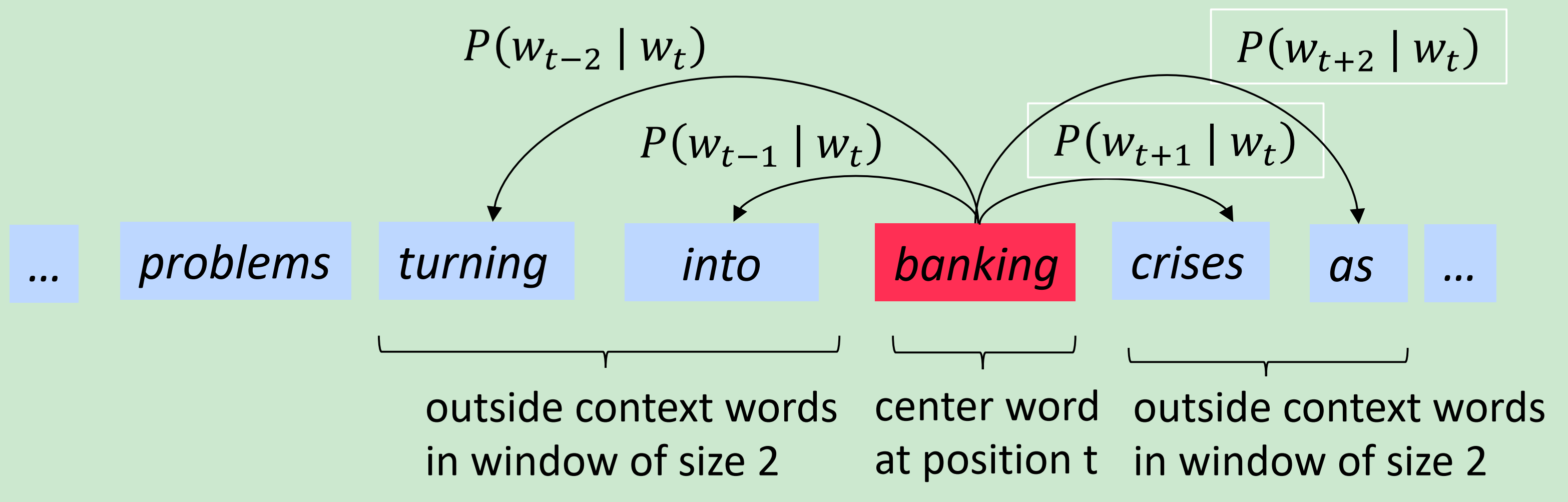
Word2vec: objective function
对于每个位置,给定中心词 预测在一个固定大小m窗口上下文
最大化的预测准确率式2,等于最小化目标函数:
Notes
基于SVD 的方法
Word-Document Matrix
矩阵X:
- 我们遍历百万级的文档,每次当单词i出现在文档j中,添加一个元素.显然这是一个规模非常大的矩阵。
- M是文档数目, V是词汇表的长度
Notes:
Distributional semantics 语义分布: 这个概念表示一个基于单词通常在上下文的意义。它是一个密度估计,这能更好地获得相似度。
以下语料库包含3句话和窗口大小为1的关系:
- I enjoy flying.
- I like NLP .
- I like deep learning.
结果的关系矩阵为:
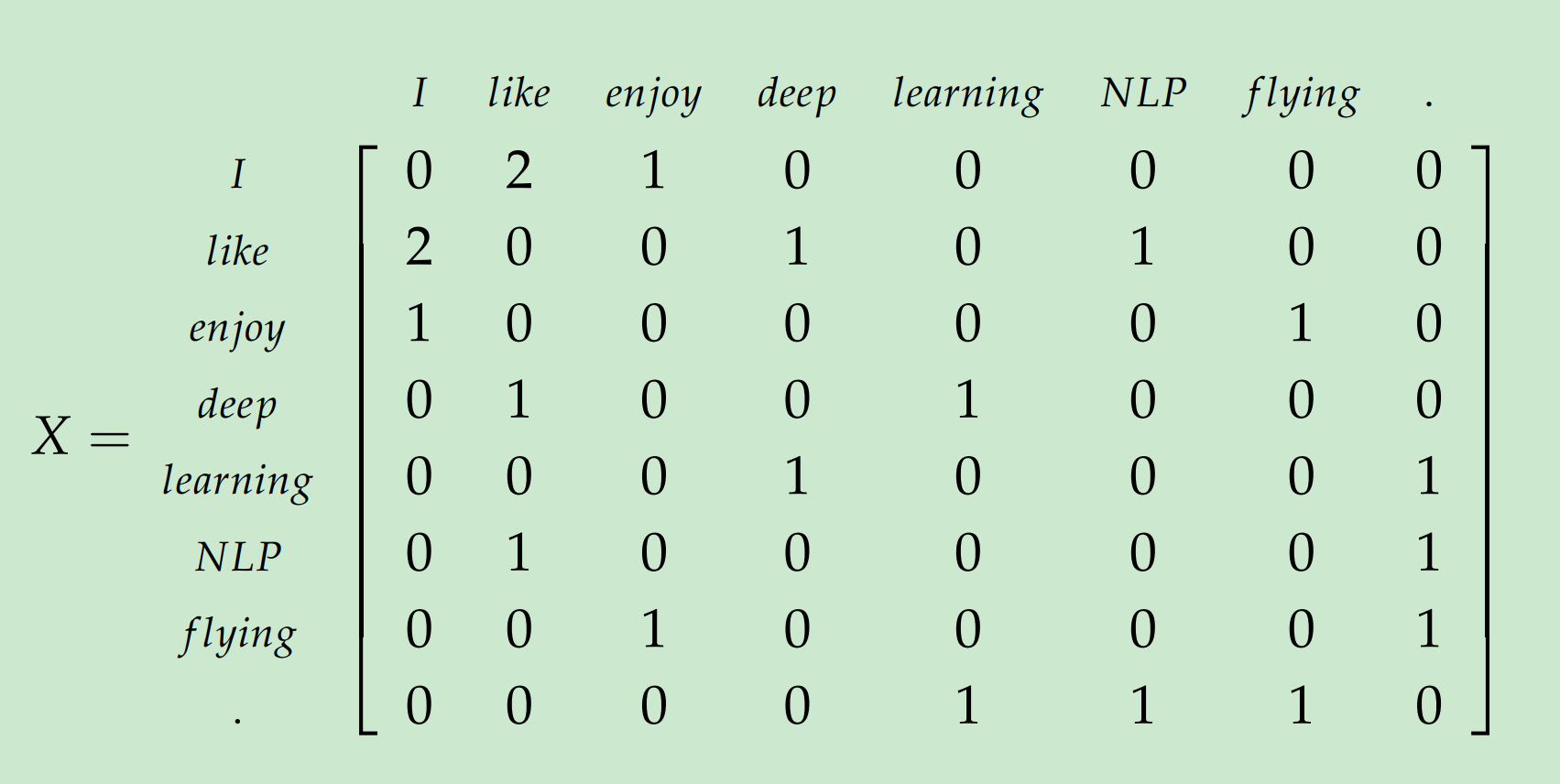
Word-Word 共现矩阵的使用:
- 生成 共现矩阵
- 对使用SVD分解得到
- 选择的前列来得到一个的词向量
- 表明通过前k维获得的方差数量
1 | import numpy as np |
Applying SVD to the cooccurrence matrix
通过对X做SVD, 观察对角阵上对角元素, 基于期望百分比方差获得前k个索引:
对X应用SVD:
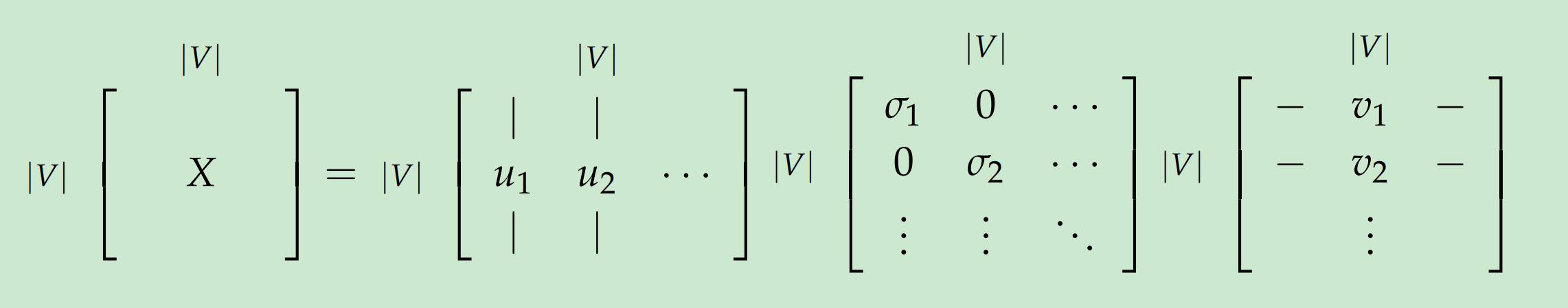
通过选择前k个奇异向量:
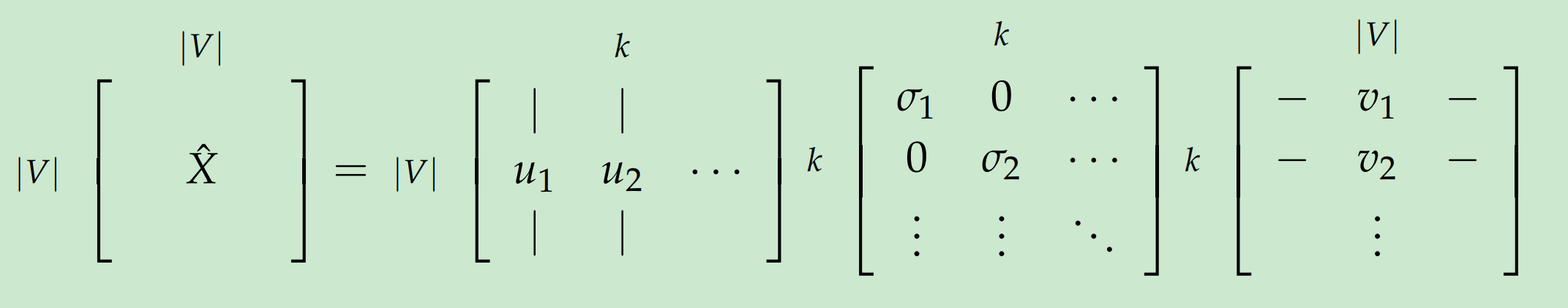
这些方法给予我们词向量, 这不仅仅足以编码语义和句法(语音部分)信息,但其引起许多其他问题:
- 矩阵维度经常变化(新词频繁加入和语料库大小变化)
- 矩阵十分稀疏,大多数词不经常出现
- 矩阵通常维度非常高()
- 平方次复杂度的训练代价(e.g 执行SVD)
- 需要在X上创建一些技巧来解决词频的急剧不平衡
一些存在来解决这些问题的措施如下:
- 忽略一些功能词如”the”, “he”, “has”, etc.
- 应用ramp window—例如,基于文档中词与词距离加上一个共现次数的权重
- 用皮尔逊系数将负数设为0而不是使用原始计数
Iteration Based Methods - Word2vec
2 algorithms : continuous bag-of-words (CBOW) and skip-gram . CBOW 目标是用周围上下文的词向量来预测中心词。Skip-gram正好相反,用中心词来预测上下文的分布或者说概率。
2 training methods :负采样或hierarchical softmax。负采样通过抽取负样本来定义目标,而hierarchical softmax用有效的树结构来对所有词汇计算概率从而定义目标。
Language Models (Unigrams, Bigrams, etc.)
Unigram model: 假设每个词出现的完全独立
Bigram model: 假定sequence 的概率取决于一个词在sequence中和其旁边词出现的概率:
Continuous Bag of Words Model (CBOW)
{“The”, “cat”, ’over”, “the’, “puddle”} 作为上下文,可以预测或生成中心词”jumped” 。——CBOW。
CBOW细节:
- 设置已知参数。令模型中已知参数用one-hot词向量表示。输入one-hot向量或上下文用,输出为。
未知参数:
创建两个矩阵,和.其中, 是由embedding 空间定义的任意维度;
是输入词矩阵,如的第列是当其是模型的输入时,对词 的 维嵌入空间向量。记为。
是输出词矩阵,如的第列是当其是模型的输出时,对词 的 维嵌入空间向量。记为。
注意: 对于每个词都学到两个向量
CBOW model:
从周围上下文来预测中心词:对每个词,我们希望学到两个向量
- 输入向量: 当这个词在上下文中
- 输出向量: 当这个词是中心词
CBOW model 记号:
- $ w_i $ 输入向量: 词汇表中的单词
- : 输入词矩阵
- : 的第列,单词 输入表示向量
- : 输出词矩阵
- : 的第行,单词 输出表示向量
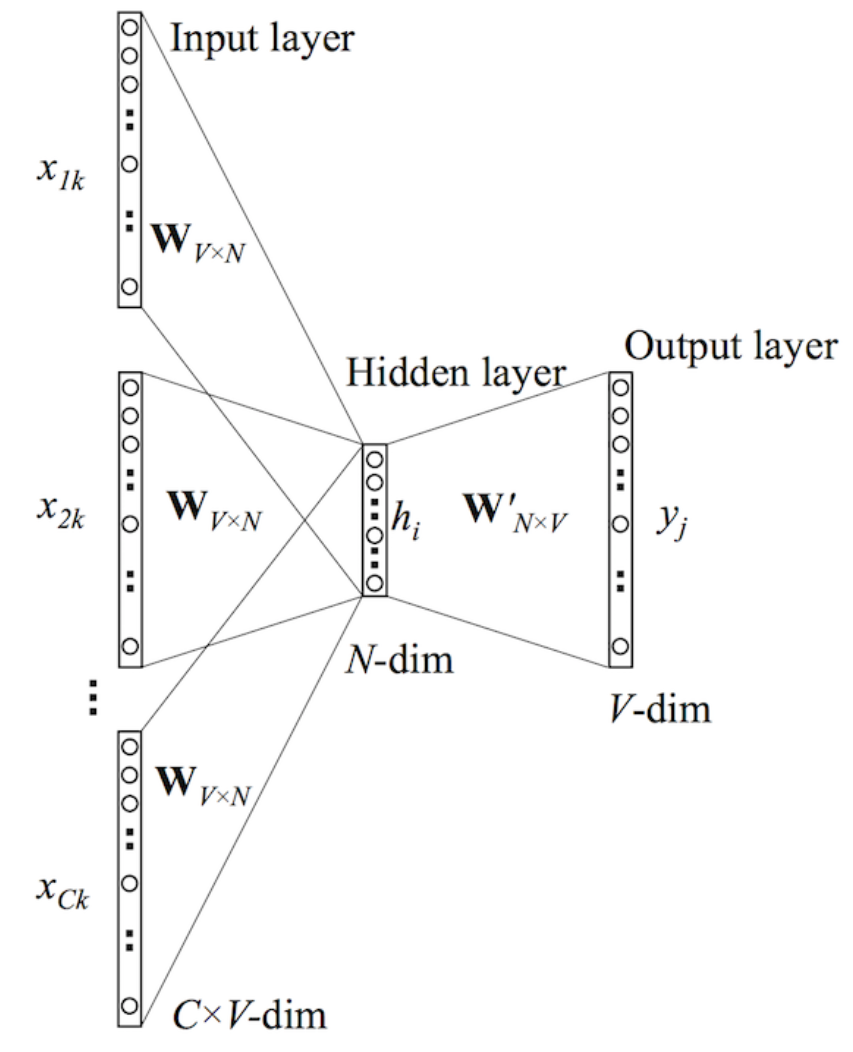
CBOW model步骤分解:
- 为输入的上下文生成大小为的one-hot词向量:, 注即中心词附近窗口内的词的词向量。
- 为上下文得到嵌入词向量
- 取这些向量的均值得到
- 生成分数向量 . 因为相似向量的点积会高(点积的几何意义),为了达到高分数, 将会迫使相似词彼此靠近。
- 将分数变为概率。
- 要求生成的概率, , 来匹配真正的概率, , 这也恰好是真实词的one-hot向量。
现在,我们了解了如果我们有模型怎么工作, 我们怎样学到这两个矩阵?
利用交叉熵来得到到loss function:
$ y $是一个one-hot 向量, 因此,可以将式7简化为:
softmax 操作 :
Note:: 。这意味着我们模型在预测中心词上是非常好的。
最小化 目标函数:
可以用随机梯度下降来更新所有有关词向量。
Skip-Gram Model
Skip-Gram Model :
- 给定中心词预测周围上下文
大部分参数设定跟CBOW一样, 不过把与 交换下。 输入one-hot向量是中心词用表示, 输出向量是周围上下文用表示。跟CBOW一样。
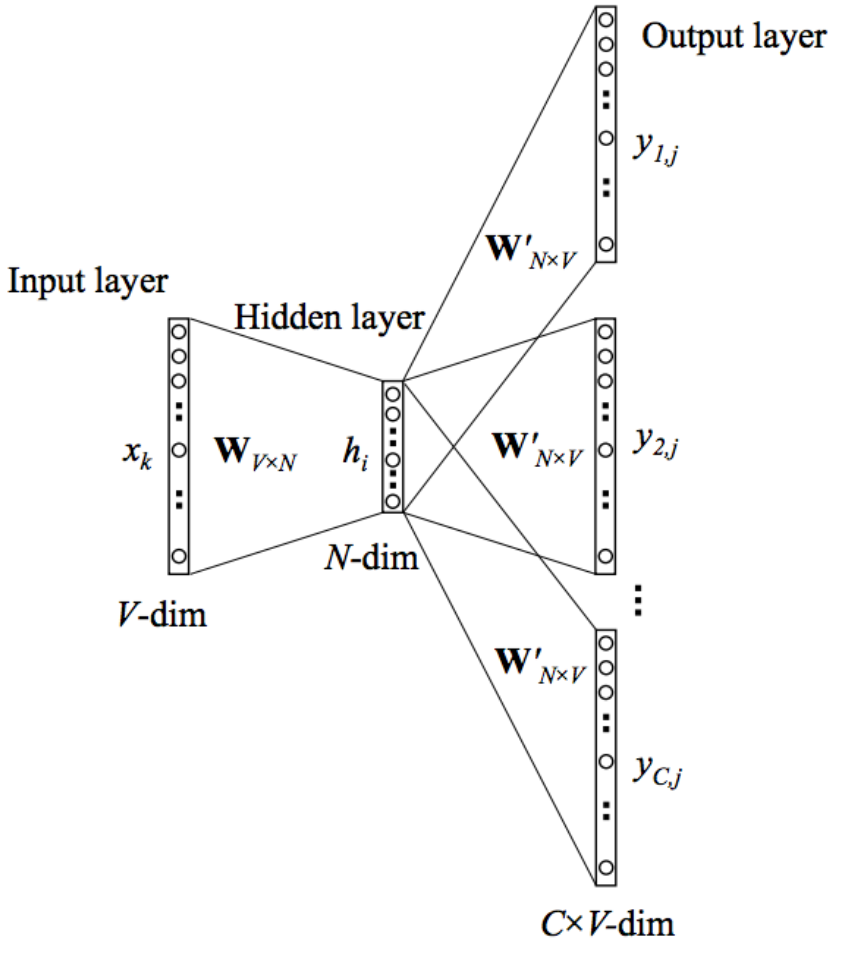
Skip-Gram model步骤分解:
- 生成中心词的one-hot输入向量。
- 中心词 的嵌入向量。
- 生成分数向量 .
- 将分数变为概率。注:是观察的每个上下文词的概率
- 要求生成的概率向量来匹配真实的概率 ,即真实输出的one-hot向量。
CBOW中,是生成目标函数来估计模型。Skip-Gram 是用朴素贝叶斯分解概率表达式, 即假定输出词是完全独立的。
利用SGD来迭代求出未知参数:
注: 仅仅只有一个概率向量要计算。Skip-gram 将每个上下词平等看待:模型计算独立地出现在中心词的每个上下词对中心词距离的概率。
Negative Sampling
注意到对的计算量巨大。做目标函数的任何更新或计算时间复杂度为O(|V|)。采用负采样可以近似,而不是计算整个词汇表。更新以下参数:
- 目标函数
- 梯度
- 更新准则
Tomas Mikolov 的《Distributed Representations of Words and Phrases and their Compositionality》论文中提出的负采样。虽然负采样是基于Skip-Gram模型,但实际上是优化不同的目标函数。考虑一对中心词和上下文。记表示来自语料数据的概率,对应地记表示不来自语料数据的概率。 接下来, 用sigmoid函数对建模:
建立一个新的目标函数,如果中心词和上下文词确实在语料库中,就最大化概率 ,如果中心词和上下文词确实不在语料库中,就最大化概率 。我们对这两个概率用一个简单的极大似然估计的方法(这里把作为模型的参数,在该例子中是和 )。
注意:最大化似然函函数等价于最小化负对数似然
注:是负语料。无意义的句子出现概率是很低的。我们可以从语料库中随机抽取负样例。
对于Skip-Gram ,给定中心词的观察的上下文词,新的目标函数为:
对于CBOW ,给定上下文词向量观察的中心词的目标函数为:
Skip-Gram对应的softmax损失:
CBOW对应的softmax损失:
上面公式中, 是从抽样得到的。实际上效果最好的是取的Unigram model,论文中取值。
Hierarchical Softmax
同样是, Tomas Mikolov 的《Distributed Representations of Words and Phrases and their Compositionality》论文中提出的Hierarchical Softmax。实际上, Hierarchical Softmax对低频词表现更好,而负采样对高频词和低维向量表现更好。
Hierarchical Softmax用二叉树表示词汇表中的所有词。树的每一个叶子节点都是一个词,并且只有一条路径从根到叶子。在该模型中,没有词的输出表示。相反, 图的每个节点, 除了根节点和叶子节点, 都跟模型要学的向量相关。
在该模型中,给定向量 单词的概率,记为,等于从根结点开始到对应 的叶结点的随机的概率。优势是时间复杂度变为O(log(|V|)),对应该路径的长度。
引入一些记号:
: 从根节点到叶子节点的路径上的节点数目。下图, 对应3.
:该路径上第i个节点向量, 即叶子节点
w到跟节点路径的第i个节点。是根节点, 而 是
w的父节点。对于每个内部节点
n, 任意选择其中一个孩子节点称为,总是左节点。
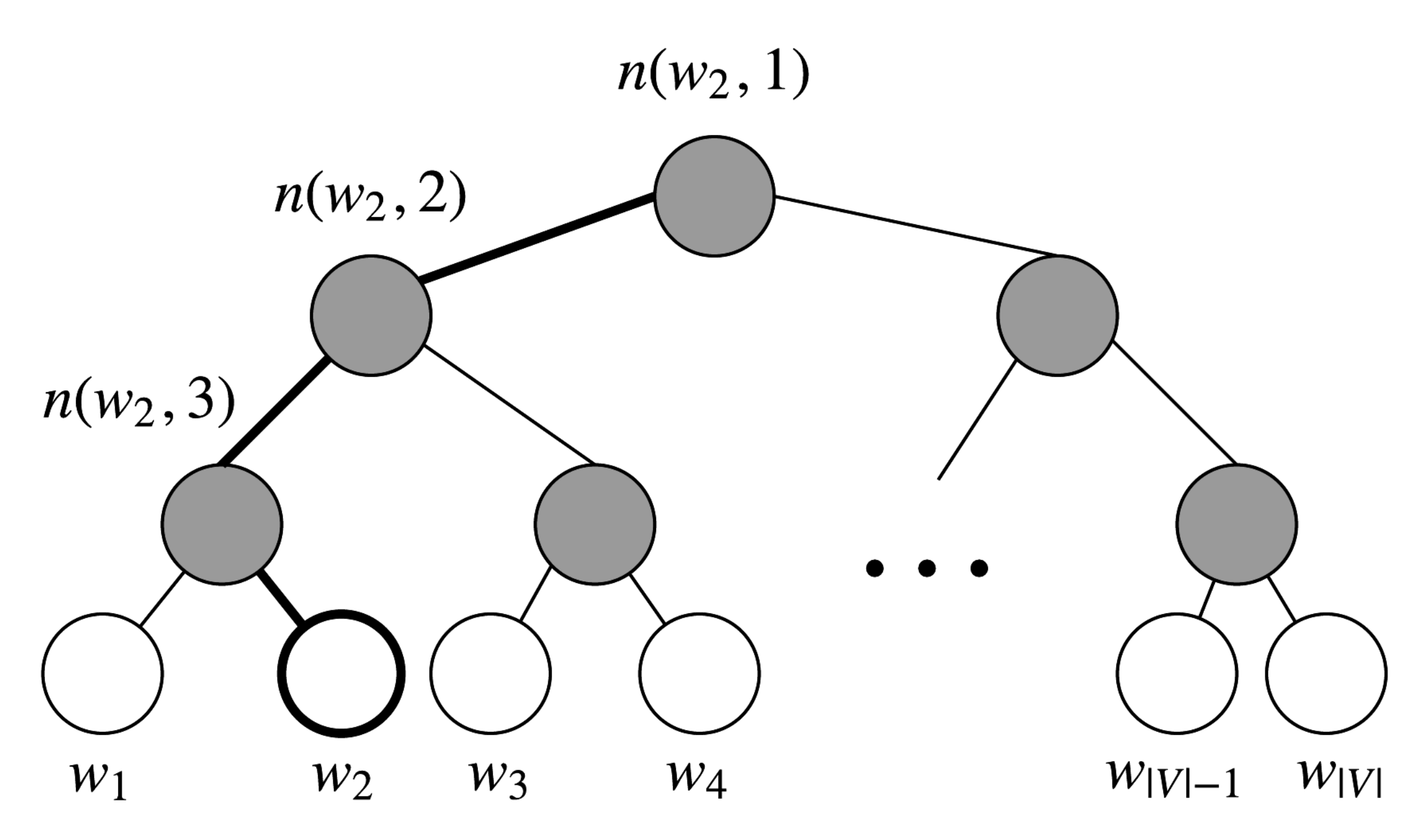
计算概率为:
这里,
式20是风采难懂的。
基于从根节点到叶子节点的累乘项。如果我们假设总是左节点, 就返回1, 反之则是-1.
提供标准化。在节点上, 如果从左节点到右节点的概率求和,对于任意的有:
同时保证了, 跟原来的softmax一样。
- 使用点积对比输入向量和每个内部节点向量相似度。例如,上图 , 我们必须要取两条左边和一条右边来从到根节点,即:
为了训练模型,我们的目标仍然是最小化负对数似然。但不是更新每个输出向量, 而是更新在二叉树上从根到叶子节点的节点向量。
该方法的速度取决于二叉树构建的方式和分配到叶子节点的单词。Mikolov 使用了哈夫曼树, 将高频词分配到树的最短路径上。
参考
[1] cs224n-2019-notes01-wordvecs1
[2] cs224n-2020-lecture01-wordvecs1
[3] CS224n课程笔记翻译 词向量I: 简介, SVD和Word2Vec
[4] Word2Vec Tutorial Part I: The Skip-Gram Model
[5] Word2Vec Tutorial Part II: The Continuous Bag-of-Words Model





